
Regressão Linear é a análise de regressão gera uma equação para descrever a relação estatística entre uma ou mais variáveis preditoras e a variável resposta. A regressão linear encontra a linha que melhor representa as variáveis de entrada com a variável de saída.
Dizemos melhor, pois como você deve ter observado nos gráficos de dispersão que realizou, é muito difícil encontrar uma linha que passe em cima de todos os dados.
Você tem duas coisas que quer relacionar – digamos, o custo de anuidades da universidade e a média de resultados dos exames finais do ensino médio dos alunos admitidos.
Você poderia pensar que escolas com resultados de exames mais elevados teriam propensão a ser mais caras. No entanto, uma olhada nos dados nos diz que essa não é uma lei universal.
A Elon University tem uma pontuação média de 1.217, e cobra uma anuidade de 20.441,00. O Guilford College cobra 23.420,00, mas a média de ingresso nos exames de conclusão é de apenas 1.131. Agora, se você as 31 universidades privadas que informaram suas anuidades e pontuações para ingresso em 2007, perceberá uma tendência clara.
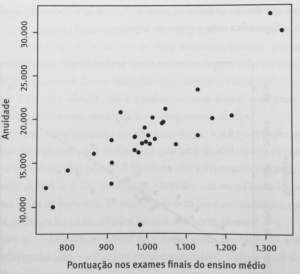
Cada ponto do gráfico representa uma das faculdades. Os dois pontos bem altos no canto superior direito, com pontuações de exames nas alturas e preços idem? Wake Forest e Davidson.
O ponto solitário perto da base, a única escola privada na lista com anuidade inferior a 10 mil, Cabarrus College.
A figura 1 mostra claramente que escolas com notas mais altas têm em geral, preços mais altos. Mais quanto mais altos? É aqui que a regressão linear entra em cena. Os pontos da figura não estão obviamente numa linha reta.
Provavelmente você poderia traçar uma linha reta a mão livre cortando muito aproximadamente o meio dessa nuvem de pontos. A regressão linear expulsa o trabalho de adivinhação, achando a reta que mais se aproxima daquela que passa por todos os pontos.
Para encontrar o que significa “mais se aproxima”, deve-se: substituir a anuidade real em cada escola pela estimativa sugerida pela reta, e então computar a diferença entre a anuidade real e a estimada para cada escola, e aí elevar ao quadrado cada um desses números e somar todos esses quadrados.
Aí você obterá uma espécie de medida total de quanto a reta está desviada em relação aos pontos, e você escolhe a reta que torna essa medida a menor possível. Quadrados? Pitágoras? A geometria subjacente à regressão linear nada mais é que o teorema de Pitágoras transposto e alçado a um contexto dimensional muito mais elevado, mas essa história requer mais álgebra do que o interesse neste momento.
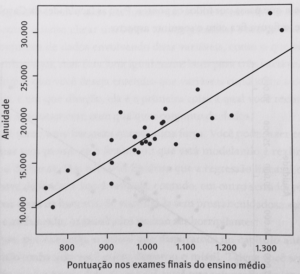
A reta na figura 2 tem uma inclinação de cerca de 28. Isto significa: se a anuidade fosse de fato totalmente determinada pela pontuação dos exames finais, cada ponto extra nos exames corresponderia a adicionar 28 dólares na anuidade. Se você puder aumentar à média nos exames dos seus calouros admitidos em cinquenta pontos, poderá cobrar US$ 1.400 a mais de anuidade. Na visão dos pais, cem pontos do filho irão lhes custar US$ 2.800 a mais por ano.
A regressão linear é uma ferramenta maravilhosa, escalável e tão fácil de executar quanto clicar um botão na sua planilha. Você pode usá-la para conjuntos de dados envolvendo duas variáveis, como o exemplo anterior, mas funciona igualmente bem para três variáveis, ou mil. Sempre que você desejar entender que variáveis conduzem a outras variáveis, e em que direção, ela é a primeira coisa à qual você recorre. E funciona absolutamente com qualquer conjunto de dados.
Porém, cuidado. Você pode fazer regressão linear sem pensar se o fenômeno que está modelando é realmente próximo de linear. Mas NÃO deve. Regressão é como uma chave de fenda, contudo, se olharmos o quão perigoso é o seu uso, é melhor compararmos ela à uma serra de bancada. Se você usá-la sem prestar cuidadosa atenção, os resultados podem ser desastrosos.
Sua reta fornece um modelo muito preciso para o movimento do míssil: para cada minuto que passa, o míssil aumenta sua altitude num valor fixo de 400 metros. Após uma hora, estará a 24 quilômetros de altitude. E quando ele desce? Não desce nunca. Uma reta inclinada ascendente segue seu rumo indefinidamente. E agora? É um novo míssil espião alienígena?
Nem toda curva é uma reta. E a curva do voo do míssil não o é. É uma parábola, lembra-se das aulas de física do colegial?
Movimento balístico não é mesmo? Exatamente como círculo de Arquimedes, ela parece uma reta quando vista de perto, e é por isso que a regressão linear faz um bom serviço dizendo-lhe onde o míssil estará cinco
segundo depois que você o rastreou da última vez. Mas e uma hora depois? Seu modelo diz que o míssil está na estratosfera, passeando pelo espaço sideral.
Mas o artigo sobre a Obesity oculta o PIOR CRIME contra a matemática e o senso comum. A regressão linear é fácil de fazer – uma vez que se fez uma, as outras são tranquilas. Então Wang e companhia dividiram seus dados segundo grupos étnicos e sexo. Homens negros, por exemplo, tinham menos propensão a estar acima do peso que o americano médio, e, mais importante, sua taxa de sobrepeso crescia apenas com metade da velocidade. Se sobrepusermos a proporção de homens negros acima do peso sobre a proporção global de americanos acima do peso, junto com a regressão linear que Wang e companhia elaboraram, veremos que homens negros são mais magros. Eles só estarão todos acima do peso em 2095. Em 2048, só 80% serão obesos.
Conseguem localizar o problema? Se todos os americanos estarão acima do peso em 2048, onde deverão estar aqueles 1 em 5 futuros homens negros sem problema de peso? No exterior? A contradição básica passa sem ser mencionada no artigo. Artigos como este me lembram das brincadeiras que fazíamos quando algum colega, numa prova de física, registrava que a altura do poste era de 5 quilômetros.
Ah Lembre-se: higiene matemática é importante. Quanto você está testando em campo um método matemático, tente computar a mesma coisa de várias maneiras diferentes. Se você obtiver respostas diferentes, há algo de errado em seu método.